1. Permutasi
Permutasi BiasaPermutasi ini
merupakan penyusunan kumpulan angka/objek dalam berbagai urutan-urutan
yang berbeda tanpa ada pengulangan. Dalam permutasi urutan diperhatikan
(tidak boleh ditukar-tempat).
Rumus Permutasi
Syarat :
r <= n (n harus lebih kecil atau sama dengan r)
Notasi :
nPr = P nr = P(n,r) = Lihat rumus di kanan-atas :D
dimana n! adalah Faktorial
Contoh soal :
1.
Sebuah dalam tim olahraga ada 10 orang siswa yang dicalonkan untuk
menjadi pemain. Namun hanya 5 orang boleh menjadi pemain utama. Tentukan
banyak cara yang bisa dipakai untuk memilih para pemain utama tersebut?
Diketahui :
Permutasi P (10,5) atau bisa juga
10P5 , n =10 dan r =5 , Maka :
Jawab : P(10,5) = n! / (n - r)!
= 10! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
(10 - 5) ! 5!
= 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 5 x 4 x 3 x 2 x 1= ... ? (tinggal dikalikan)
Ingat Faktorial dari n bilangan adalah deret perkalian bilangan sebelumnya dan bilangan itu.
5! = 5 x 4 x 3 x 2 x 1
Permutasi Unsur Sama
Jika
permutasi diatas tidak ada unsur yang sama alias tiap element
berbeda-beda. maka ada juga permutasi dengan elemen yang sama misalnya
pada kata
MATEMATIKA dimana terdapat 3 huruf A, 2 huruf M dan 2 huruf T . Maka rumus nya nya
n! r1! x r2! x ri!......
jadi kata MATEMATIKA di kerjakan seperti ini :
Dik : n = 10 (total huruf nya)
r1 = 3 , r2 = 2, r3 = 2
10! 3! x 2! x 2!
=
Permutasi Siklik
Permutasi
siklis adalah permutasi yang dibuat dengan menyusun unsur secara
melingkar menurut arah putaran tertentu. sangat umum Soalnya biasanya
tentang sususan orang di meja makan, meja rapat dsb.
Rumus nya sederhana :
(n-1)! , dimana n adalah jumlah object/orang yang ada
contoh : 5 orang direktur duduk disebuah meja berbentuk lingkaran untuk rapat. Ada berapa cara untuk menyusun kursi para direktur tersebut?
Jawab :
(5-1)! = 4! = 4 x 3 x 2 x 1 = 24
2.Perkalian
Sebelum
menuju ke kaidah perkalian kita awali dengan pengamatan percobaan sederhana.
Sebuah diagram pohon dapat digunakan dalam perhitungan ruang sampel. Misalnya
pada percobaan 2 kali pelemparan sebuah mata uang. Himpunan hasil yang mungkin
dapat diperoleh oleh seluruh garis yang ditunjukkan dalam diagram pohon
berikut.
Dalam
setiap percobaan ada 2 kemungkinan hasil angka (A) atau gambar
(G). Percobaan dengan 2 kali pelemparan mata uang didapat hasil
sebanyak 22 = 4 buah titik sampel. Jadi ruang sampel
S = {GG,
GA, AG, AA}.
Jika
dari kota A menuju kota B ada 3 jalan yaitu jalur p, q, atau r
sedangkan dari kota B ke kota C ada 2 jalan yaitu jalur a atau b maka
dari kota A ke kota C dapat ditempuh melalui 3 x 2 jalur yang berbeda, yaitu:
S
= { (p ,a), (p ,b), (q
,a), (q ,b), (r ,a), (r ,b) }
Selanjutnya
akan kita pelajari suatu kaidah yang berkaitan dengan percobaan seperti contoh
di atas.
Dalam
melakukan dua percobaan, kaidah perkalian mengatakan bahwa:
Jika
satu percobaan memiliki m hasil yang mungkin dan percobaan yang lain
memiliki n hasil yang mungkin, maka jika dua percobaan tersebut
dilakukan bersamaan memiliki mn hasil yang mungkin.
Contoh Soal:
1.) Bila sepasang dadu dilemparkan sekali, berapa banyak titik sampel
dalam ruang sampelnya ?.
Jawab :
Jika
sepasang dadu dilemparkan satu kali maka dadu pertama akan muncul 6 cara
sedangkan dadu kedua .akan muncul 6 cara juga
Dengan
demikian, sepasang dadu tersebut dapat terjadi dalam 6 × 6 = 36 cara.
2.) Sebuah
dadu dan sebuah uang logam dilempar secara bersamaan, hasil yang mungkin
adalah:
- Untuk dadu; jika hasil dari
lemparan mata dadu adalah 1, 2, 3, 4, 5, 6, maka ada 6 hasil yang mungkin,
- Untuk uang logam; jika hasil
lemparan uang logam ada gambar dan angka, maka ada 2 hasil
yang mungkin.
Sehingga
dengan kaidah perkalian diperoleh banyaknya elemen dari ruang sampel ada 6 × 2
= 12 hasil yang mungkin.
3,) Diketahui empat angka 1, 3, 4, 9
tentukan banyaknya bilangan yang dapat dibuat dari angka tersebut yang terdiri
dari
a. 2 angka / digit.
b. 2 angka tetapi tidak boleh ada angka yang sama.
Penyelesaian :
a. Untuk mempermudah sediakan dua
kotak yang akan diisi jumlah kemungkinan tiap kotak, yaitu kotak pertama untuk
letak angka puluhan dan kotak kedua untuk angka satuan.
Gambar
1.2.2 Menyusun dua angka pada deretan dua kotak
Kotak pertama ada 4 kemungkinan angka. Kotak kedua ada 4
kemungkinan, karena angka yang muncul di kotak pertama boleh muncul di kotak
kedua. Jadi banyaknya bilangan yang dimaksud adalah 4 × 4 = 16.
b. Dengan cara yang sama dengan penyelesaian soal 1, tetapi
karena tidak boleh sama angkanya maka kalau angka puluhan sudah muncul
kemungkinan angka satuannya berkurang satu dan jumlah kemungkinannya adalah 4 ×
3 = 12.
Permutasi
Dan Kombinasi
Notasi
Faktorial
Hasil
kali dari bilangan-bilangan bulat positif dari 1 sampai dengan n, yaitu
1×2×3×4
· … × (n-2) × (n-1) ×n
sering
digunakan dalam matematika. Dan selanjutnya buat definisi sebagai berikut.
Untuk sembarang bilangan bulat , n faktorial yang ditulis n!, didefinisikan sebagai:
n! = n × (n-1) × (n-2)
× … ×3×2×1 Dan didefinisikan 0!=1.
Dari
definisi n!, dapat dicari persamaan berikut ini.
Contoh :
4!
= 4×3×2×1 = 24.
6!
= 6.5! = 6×5×4×3×2×1 = 720.
Permutasi
1.)Permutasi tanpa ulangan
Permutasi berkaitan dengan pengaturan suatu susunan yang dibentuk
oleh keseluruhan atau sebagian dari sekumpulan objek tanpa ada pengulangan.
Susunan pada permutasi memperhatikan urutannya.
Contoh:
-.) Untuk
mengatur 3 huruf A, B dan C secara berurutan, didapat hasil yang mungkin adalah
: ABC, ACB, BAC, BCA, CAB, dan CBA. Masing-masing urutan ini dinamakan permutasi
dari 3 obyek berbeda yaitu: A, B dan C. Jadi banyaknya permutasi dari 3 obyek
berbeda ada 6.
Misal,
diberikan n obyek berbeda. Banyaknya permutasi n obyek tersebut
dapat dihitung sebagai berikut:
- untuk mengisi posisi urutan
pertama ada n cara berbeda,
- untuk mengisi posisi urutan kedua
ada n-1 cara berbeda,
- untuk mengisi posisi urutan ketiga
ada n-2 cara berbeda,
. . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
- untuk mengisi posisi urutan ke-r
ada n-(r-1) cara berbeda,
. . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
- untuk mengisi posisi urutan ke-n
ada n-(n-1)=1 cara berbeda.
Sehingga dengan kaidah perkalian
diperoleh banyaknya permutasi adalah
n×(n-1) ×(n-2) ×(n-3) × … × 3×2×1 = n!
Suatu pengaturan susunan/urutan r objek tanpa pengulangan
yang dibentuk dari n objek berbeda, dengan n lebih besar sama
dengan r, dinamakan permutasi r objek dari n objek.
Banyaknya permutasi ini disimbulkan dengan P(n,r).
Jika
r=n maka banyaknya permutasi n objek yang berbeda adalah P(n,n)
= n!. Lihat penjelasan sebelum definisi dan definisi dari permutasi.
2,) Permutasi Dengan Pengulangan
Permutasi
dengan pengulangan merupakan permutasi r objek dari n buah objek
yang tidak harus berbeda. Beda dengan sebelumnya yang n buah objeknya
berbeda. Sebelum menghitung banyaknya permutasi dengan pengulangan ini,
terlebih dahulu kita lihat contoh berikut ini.
Tentukan
ada berapa cara untuk menyusun berjajar huruf-huruf yang terdapat dalam sebuah
kata "PEPPER"!
Penyelesaian:
Jika
3 huruf P dan 2 huruf E dapat dibedakan, maka ada sebanyak cara berbeda yang
mungkin.
Akan
tetapi, jika 3 huruf P tidak dapat dibedakan, maka 3! susunan yang dibentuk
dari 3 huruf P diwakili/dihitung satu saja. Sehingga banyaknya susunan yang ada
harus dibagi 3!, akibat 3 huruf P yang kembar.
Secara
sama, jika 2 huruf E tidak dapat dibedakan, maka 2! susunan yang dibentuk dari
2 huruf E diwakili/dihitung satu saja. Sehingga banyaknya susunan yang ada
harus dibagi lagi dengan 2!, akibat 2 huruf E yang kembar.
Jadi
banyaknya cara menyusun menyusun huruf-huruf tersebut ada sebanyak
 adalah
adalah 
 adalah ...
adalah ...
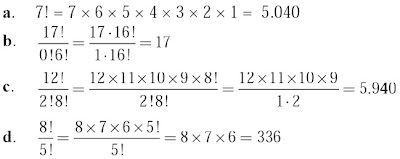
 .
.


